 [Image: Jan Curtis].
[Image: Jan Curtis].
The Northern Lights are on the move.
“The Earth’s north magnetic pole is drifting away from North America so fast that it could end up in Siberia within 50 years, scientists have said.”
 [Image: Jan Curtis].
[Image: Jan Curtis].
“The shift could mean that Alaska will lose its northern lights, or auroras, which might then be more visible in areas of Siberia and Europe” – including, of course, the cities: Northern Lights coiling above cathedrals, bus routes, and sidewalk cafes.
 [Image: Jan Curtis; see BLDGBLOG’s Radio Aurora New York for another].
[Image: Jan Curtis; see BLDGBLOG’s Radio Aurora New York for another].
Auroras have already been spotted as far south as Rome, crackling above the Pantheon; following these recent, accelerating movements of the earth’s magnetic field, however, Roman auroras might occur every night.
Hotel rates will skyrocket.
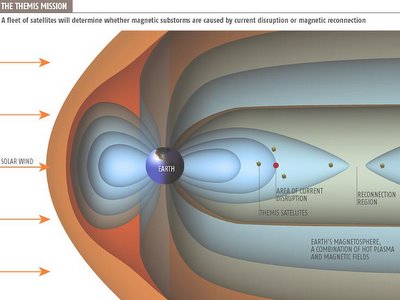 [Image: “The magnetosphere is a kind of elastic fire. It forms where the Earth’s magnetic field meets the hot plasma – the ionised gases – at the edge of the planet’s atmosphere.” It is “occasionally rocked by an explosive convulsion that flings some of its energies at the Earth, switching on spectacular auroras, damaging satellites, and knocking out electric power grids”].
[Image: “The magnetosphere is a kind of elastic fire. It forms where the Earth’s magnetic field meets the hot plasma – the ionised gases – at the edge of the planet’s atmosphere.” It is “occasionally rocked by an explosive convulsion that flings some of its energies at the Earth, switching on spectacular auroras, damaging satellites, and knocking out electric power grids”].
At least one possible architectural project here would be to construct a tower of some sort, or a superstadium full of ring magnets and electromagnetic coils; these would attract, then trap, the planet’s north magnetic pole.
The pole would be permanently anchored; its terrestrial migration – and ultimate reversal – would stop.
The stadium would hum quietly, and all compasses would point toward it.
Massive sheets of auroral light would then torque downward every night at high speed – breaking away at the last minute to fold off toward the suburbs. You could stand on the roof and drink beer with your mates. Forget fireworks.
It’s a Project for a New North Pole.
I think this was bound to happen after so many, many close calls in the past.
Goodbye, Alaska!
So tell me what I’m thinking… right now!
(What are you posting next? If we overlap again I’m calling a doctor)
How to make Indian highways sing to the tune of colliding tectonic plates? Am too shellshocked to speculate further.
I have two on mapping in the works, but now it’s probably best to wait until our brainwaves depolarize.
Please don’t psychovideograph my dreams while I sleep tonight.
Too late – and you have a sick mind, Mr. Trevi.
You could build a smaller version – a backyard grill – full of electromagnetic coils and turn it on for your own light display. It would attarct the earth’s magnetic field and make auroras while you grilled supper. Also a coffee table full of magnets you turn on and the auroras appear in your home, a new kind of TV. Or an antenna you attach to your pick-up truck and the auroras follow you down the highway. Turn it into a cinema and make pictures in the sky.
happily clueless as to the technical side of this: but wouldn’t it be possible to build yr megacoil aurora-sucking stadium (ideally w/ teslamaginary wireless electricity based on vril earth energy) then just use all the magnetic force to airfloat a flotilla city like the one in scar (and neil stephenson’s diamond age too) out of boxcars, fuselages, salvage freight carriers, cathedralchunks dipped in iron, and plenty of dome-homes? spliced together with magnetized sidewalks, traversed on ziplines, poles, and ladders, maze of trapdoors and springloaded catapult platforms? i’d live there anyday, and it seems feasible.
one of my life goals was to make a pilgrimage to see aurora, but I’ll just sit around and wait for it, or build something like a magnetic coffee table/grill on wheels.
I don’t know about the air-floating, but you could surely do a kind of Icelandic geothermal-energy design, only using the earth’s magnetic field instead: it would power the city’s trains and subways, light homes, keep the sewers working, rearrange churches (naves of origami, changing spires, glowing domes). Fritz Lang’s Metropolis meets China Miéville via Jules Verne’s 30th-century Paris, as designed by Nikola Tesla and BLDGBLOG. Throw in some Antonio Sant’Elia and several city blocks specially reserved for the Museum of Ephemerata. Everyone is given a special aurora-attracting backyard grill. The city shimmers, crackles and pops. At its heart, the auroral coloseum, with ring magnets beneath every seat. The Super Bowl is played there. The sky snakes above the crowd in red and orange and blue and green trails of geomagnetic energy.
Etc.
Wouldn’t our watches, computers, iJunk &c. have some trouble in the proximity of this megamagnet?
It would be a timeless display.
You could build a smaller version – a backyard grill – full of electromagnetic coils and turn it on for your own light display. It would attarct the earth’s magnetic field and make auroras while you grilled supper. Also a coffee table full of magnets you turn on and the auroras appear in your home, a new kind of TV. Or an antenna you attach to your pick-up truck and the auroras follow you down the highway. Turn it into a cinema and make pictures in the sky.
You can already buy them: http://www-toys.science.unitn.it/toys/en-html/en-e-plasma.html
Sadly, you dont see the northern lights well from a city because the city lights illuminate the sky too much. Thats the case here in Iceland anyway.